What is A/B testing?
At lastminute.com we aim to provide a website that gives the best possible customer experience. We are therefore always trying to find ways to improve our website and the algorithms that drive it. First, we hypothesise a change that will improve a user’s experience, we then test it on our customer base with A/B testing. For example, in the case that we have two different versions of the website we want to test, each customer that enters the website is randomly assigned a variant, either A or B. We then measure which of these variants performs best and, when we have enough evidence, put the winning version into our site for future customers. This can be extended across many simultaneous hypothesis tests, allowing us to quickly and efficiently improve our website in a robust scientific manner.
Why is it so important?
The main difficulty in deciding which variant is best comes from the inherently noisy nature of measuring its performance. Say we want to improve a widget on the website, so as to increase the click-through rate of our users. Measurements of this performance metric consist of individual clicks. This gives a stochastic signal that is very prone to statistical fluctuations. We therefore need to make sure we collect enough unbiased data to be able to figure out which variant of the widget has the best click-through rate. The great thing about A/B testing is that it provides an unbiased way to randomly sample the different versions. It then allows us to apply statistically robust techniques to measure the different KPIs we want to test.
The statistical approaches we are using at lastminute.com
To make a quantitative decision about which variant is best we rely on different statistical approaches. Each of these approaches tells us which variant performs better (or if they perform equally) to a certain degree of belief. There are many statistical techniques for measuring things in A/B testing, so we make sure to choose the right one to answer the right question. Broadly there are two schools of thought: Frequentist and Bayesian. They both approach the problem from a slightly different angle and have different advantages and disadvantages.
Frequentist approaches
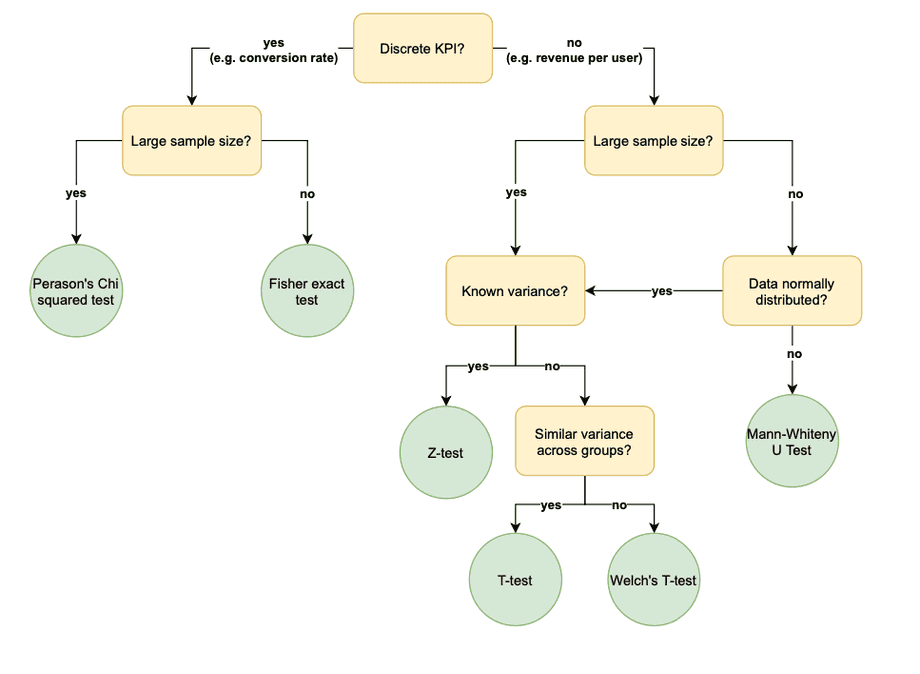
To carry out a frequentist statistical test we first define the null hypothesis, i.e. that there is no difference between the performance of version A or B. Given the data we have collected, we then calculate a p-value, which gives us the probability of obtaining test results at least as extreme as the result actually observed, under the assumption that the null hypothesis is correct [1]. If we observe a p-value less than 5%, we reject our null hypothesis and choose the best version as the winner. To avoid bias in the frequentist testing, we can only calculate this p-value once per experiment. If we decide we want to collect more data, we have to start again from scratch. For this reason we generally predefine the runtime of the experiment, to have enough data to reject the null hypothesis given a reasonable difference between the two versions. As there are many techniques for carrying out frequentist tests, from T-tests to Chi squared tests, we make a decision depending on the particular problem we are trying to answer. For example, based on this flowchart:
Bayesian approaches
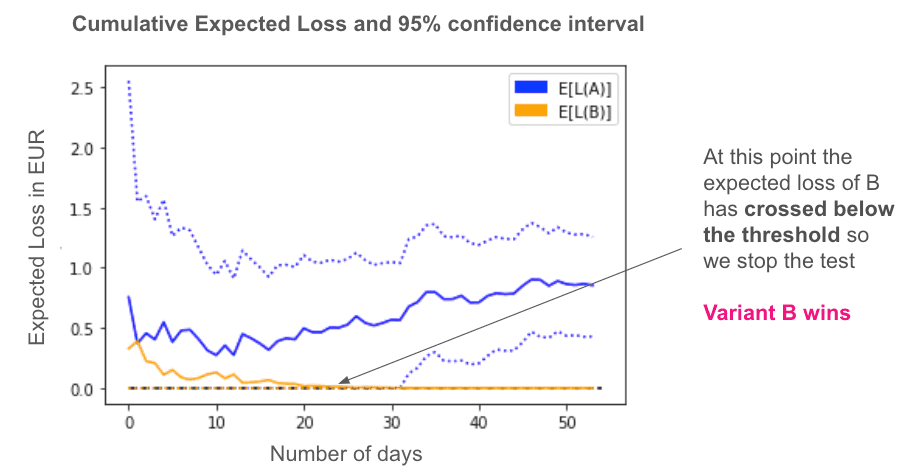
Bayesian approaches answer a different question than frequentist approaches. They don’t try to confirm or reject the null hypothesis, instead they quantify how much you expect to lose if you choose the wrong variant. This is known as the “Expected Loss”, and allows us to continuously evaluate the test and pick a variant when its expected loss passes below a certain threshold [2]. To carry out a Bayesian statistical test, first we define our prior beliefs of the performance of each variant we want to test. We then continuously update (e.g. daily) the priors based on the observations we make of the performance of each variant. An example result of a Bayesian test can be seen here:
The advantages of the different approaches
Both Frequentist and Bayesian approaches have different advantages and disadvantages. Bayesian approaches generally converge faster in many scenarios. They also allow for continuous monitoring of performances in a statistically robust way with a more intuitive interpretation, in the form of the expected loss. However, they can’t be applied to all scenarios, for example measuring revenue per user when revenues can be negative. Frequentist approaches, on the other hand, are more widely used and very robust if set up properly. They are also better for making sequential design decisions, as they give a more definitive answer as to whether A or B is better. However, it is necessary to predefine the length of a frequentist test before it is started – you shouldn’t peek at the p-value before a test is over. This makes frequentist tests slower, especially in cases when one variant is clearly better than the other.
References
[1] https://en.wikipedia.org/wiki/P-value
[2] https://vwo.com/downloads/VWO_SmartStats_technical_whitepaper.pdf
